What is Time Complexity And Why is it Essential?

jaro education
15, June 2024
6:30 pm

Time complexity is an important concept in computer science that measures the efficiency of algorithms in terms of the amount of time they take to run as a function of the size of their input. It provides a standardized way to analyze and compare algorithms, helping developers make informed decisions about which algorithm to use for a given problem.

Understanding time complexity allows programmers to predict how an algorithm will perform as the input size grows, enabling them to write efficient code that scales well and meets the performance requirements of real-world applications.

Defining Time Complexity

Time complexity measures the time an algorithm takes to execute as a function of the length of its input. It quantifies the efficiency of an algorithm by assessing the time required to execute each statement within it. For instance, if a statement is executed repeatedly, the time complexity considers the number of times the statement is executed multiplied by the time required for each execution. It is crucial for assessing algorithm efficiency, as it allows developers to understand how the algorithm’s performance scales with increasing input size. Algorithms with lower time complexity are generally preferred, as they can handle larger inputs more efficiently.

Evaluating Time Complexity

Time complexity, often expressed using Big-O notation, quantifies the amount of work a function needs to do relative to the size of its input. Big-O notation represents the complexity of a function through a mathematical expression involving variables.

In this notation, the letter “O” stands for “order,” and it precedes a variable in the expression denoting how frequently the variable appears in an equation. For instance, to determine the workload of a function concerning its input size, we employ formulas like this: ƒ(x) = O(x).

Example Illustration

Consider two algorithms: one that prints a statement once and another that prints the same statement within a loop. The first algorithm consistently takes the same amount of time to execute, while the second algorithm’s execution time increases proportionally with the number of iterations in the loop. This illustrates how the structure of an algorithm, including loop iterations and nested loops, influences its time complexity.

By understanding and analyzing time complexity, developers can make informed decisions about algorithm selection and optimization, ensuring efficient utilization of computational resources across various computing environments.

Different Types of Time Complexity

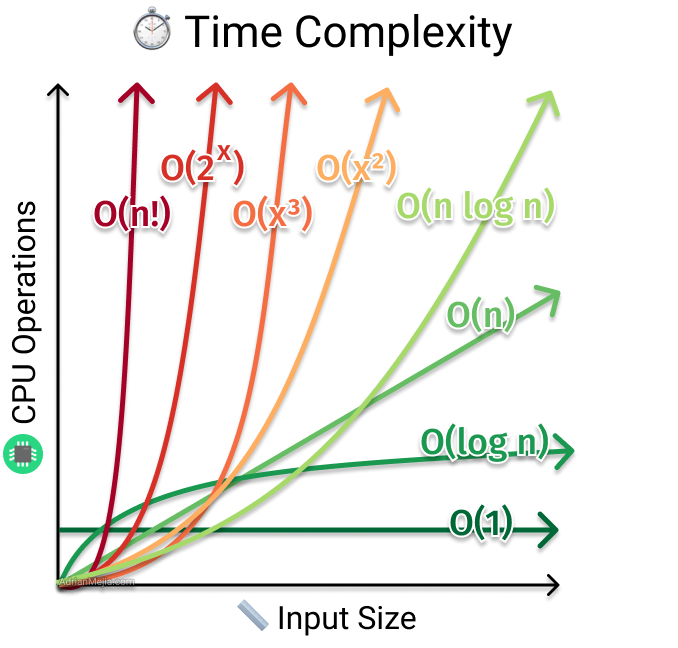
When analyzing algorithms, it’s crucial to assess their efficiency, which is often quantified through time complexity. It defines how the runtime of an algorithm grows as the input size increases. Let’s delve into various types of time complexity:

*miro.medium.com

1. Constant Time Complexity - O(1)

In constant time complexity, denoted as O(1), an algorithm’s runtime remains consistent regardless of the input size. This property is fundamental, ensuring that as long as there’s sufficient memory, the algorithm can process inputs of any size efficiently.

2. Logarithmic Time Complexity - O(log n)

Logarithmic time complexity, expressed as O(log n), indicates that the algorithm’s runtime grows logarithmically with the input size. Despite the seemingly intricate description, this complexity arises from requiring an additional operation for each item added to the input. While slightly harder to grasp due to the notation, algorithms with logarithmic time complexity are efficient.

3. Linear Time Complexity - O(n)

Linear time complexity, O(n), signifies that the algorithm’s runtime increases linearly with the input size. Each input item requires a constant amount of processing time, resulting in a proportional increase in runtime as the input size expands.

4. O(n log n) Time Complexity

Algorithms with O(n log n) time complexity exhibit runtime proportional to the logarithm of the input size multiplied by the input size itself. This complexity strikes a balance, offering better performance compared to linear time algorithms as the input size grows.

5. Quadratic Time Complexity - O(n^2)

Quadratic time complexity, also known as O(n^2), implies that the algorithm’s runtime grows quadratically with the input size. This often arises when each input requires more computational steps or when processing each input entails additional steps. Algorithms with quadratic time complexity become inefficient with large input sizes due to the substantial increase in processing time.

Factors Affecting Time Complexity of Algorithms

Several factors influence the time complexity of algorithms, determining the efficiency of their execution. Understanding these factors is crucial for analyzing algorithm performance and optimizing them for specific use cases. Here are the factors that affect the time complexity of algorithms.

Input Size: The size of the input data directly affects the time required for processing. Generally, as the input size increases, so does the time complexity. Algorithms may exhibit different behaviors based on small or large datasets.
Algorithmic Design: The design of the algorithm itself plays a fundamental role. Different algorithms have distinct complexities. For instance, linear search operates with a time complexity of O(n), meaning its execution time increases linearly with input size, whereas binary search boasts a complexity of O(log n), enabling quicker search operations.
Data Structure: The choice of data structure for storing and manipulating data significantly impacts time complexity. Utilizing appropriate data structures can lead to more efficient algorithms. For example, employing a hash table for certain operations may result in faster lookup times than using arrays or linked lists.
Hardware: The hardware environment in which an algorithm executes also influences its time complexity. Factors such as processor speed, memory capacity, and storage speed affect execution times. Faster hardware generally results in quicker algorithm execution.
Implementation: The specific implementation details of an algorithm can impact its time complexity. Choices such as using recursion versus iteration or employing efficient algorithms for fundamental operations can affect overall performance. Optimizing implementations can lead to significant improvements in execution time.

Time Complexity of Popular Algorithms

Sorting Algorithms

Quick Sort: Renowned for its efficiency, Quick Sort exhibits a time complexity of O(n log n), rendering it well-suited for handling large datasets.
Merge Sort: Recognized for its stability in sorting, Merge Sort also operates with a time complexity of O(n log n), making it a dependable choice for various scenarios.
Bubble Sort: While simple to implement, Bubble Sort’s time complexity of O(n²) makes it less efficient, particularly for larger datasets.

Search Algorithms

Binary Search: Leveraging the property of sorted arrays, Binary Search boasts a time complexity of O(log n), which makes it highly efficient for locating elements within sorted collections.
Linear Search: Despite its simplicity, Linear Search exhibits a time complexity of O(n), which can result in reduced efficiency, especially for larger datasets.

Limitations of Time Complexity

While time complexity is crucial for assessing algorithm efficiency, it has inherent limitations:

Simplistic Model: Assumes constant time for basic operations, neglecting real-world variations in execution time.
Ignoring Constant Factors: Disregards constant factors, which can significantly affect actual running time, especially for small input sizes.
Worst-case Analysis: This relies on the worst-case scenario, which may not accurately represent actual performance due to input size and distribution.
Limited Scope: Solely provides an estimate of algorithmic performance, disregarding factors like memory usage, network latency, and input/output operations.
Domain-Specific Factors: Algorithm performance can be influenced by domain-specific factors such as data structures and optimizations, which time complexity analysis may not capture adequately.

Recognizing these limitations underscores the importance of employing complementary metrics to comprehensively evaluate algorithm performance.

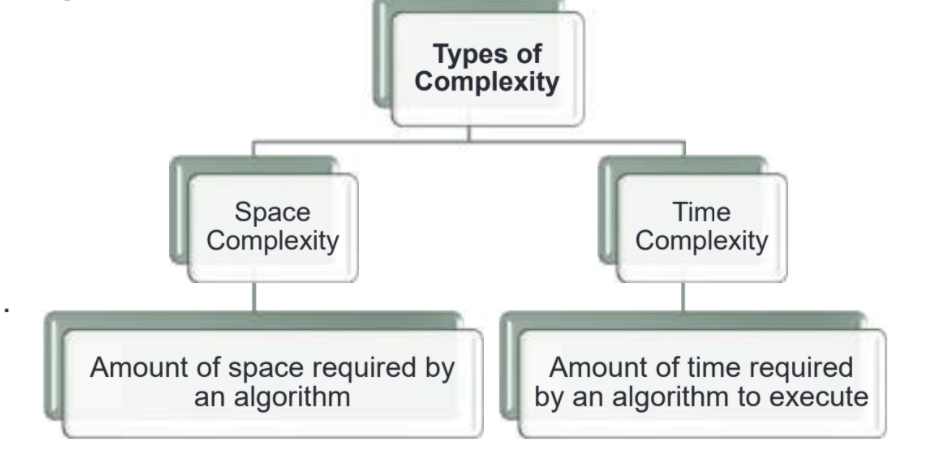
Comparisons Between Complexity in Space and Time

A fundamental aspect of algorithm design is the trade-off between space and temporal complexity, which forces resource allocation decisions to be made strategically. Achieving the best algorithmic performance and efficiency requires striking a balance between memory utilization and execution time.

*eduonix.com

Space Complexity: This metric gauges the memory required by an algorithm to solve a problem. Efficient space utilization minimizes memory consumption by employing techniques such as reusing memory, discarding unnecessary data, or optimizing data structures.

Time Complexity: Focusing on computational efficiency, time complexity measures the time required for algorithm execution. Time-efficient algorithms minimize operations or iterations needed to solve a problem, ensuring faster execution.

The trade-off arises as reducing one often impacts the other. Techniques such as precomputing values or caching results enhance time efficiency but increase space requirements. Conversely, minimizing memory usage may lead to longer execution times by recalculating values on the fly.

The choice between space and time optimization depends on problem requirements and system constraints. Limited memory resources may necessitate prioritizing space efficiency, while time-critical scenarios may emphasize time optimization, even at the expense of increased memory usage.

Conclusion

Understanding time complexity is important in algorithm design, enabling developers to craft efficient solutions that scale gracefully with increasing input sizes. By quantifying the relationship between runtime and input size, time complexity analysis facilitates informed algorithm selection and optimization. However, it’s crucial to recognize the limitations of time complexity and complement it with other metrics for a comprehensive evaluation of algorithm performance.

If you want to learn further about different computational topics, Executive Certification in Advanced Data Science & Applications by IITM Pravartak is the right choice. Through a blend of theoretical insights and practical case studies drawn from diverse business sectors, this interdisciplinary program equips participants with a contextual understanding of various relevant topics. By immersing professionals in intensive self-study applications that leverage various techniques on real-world data, the curriculum ensures that learners grasp the fundamental methods and tools essential for staying ahead in the AI revolution.