Mastering Number Patterns in C: A Programmer’s Guide
Table of Contents

- jaro education
- 14, June 2024
- 10:00 am
A number pattern is a series of numbers that are arranged in a specific order. In programming, number patterns form an essential part of algorithm thinking and problem-solving. Developing number patterns in C is a key component in learning the entire programming itself. With these patterns, developers and coders can learn different C programming principles.
Here, we will learn about number patterns in C++. Furthermore, we will also explore how to create appealing visual designs using loops and conditionals. There is a wide range of number patterns in C, which will be covered, from squares and triangles to intricate pyramids, diamond shapes and spirals. Each pattern will include a full description and C++ code to assist readers in understanding and implementing these engaging patterns.
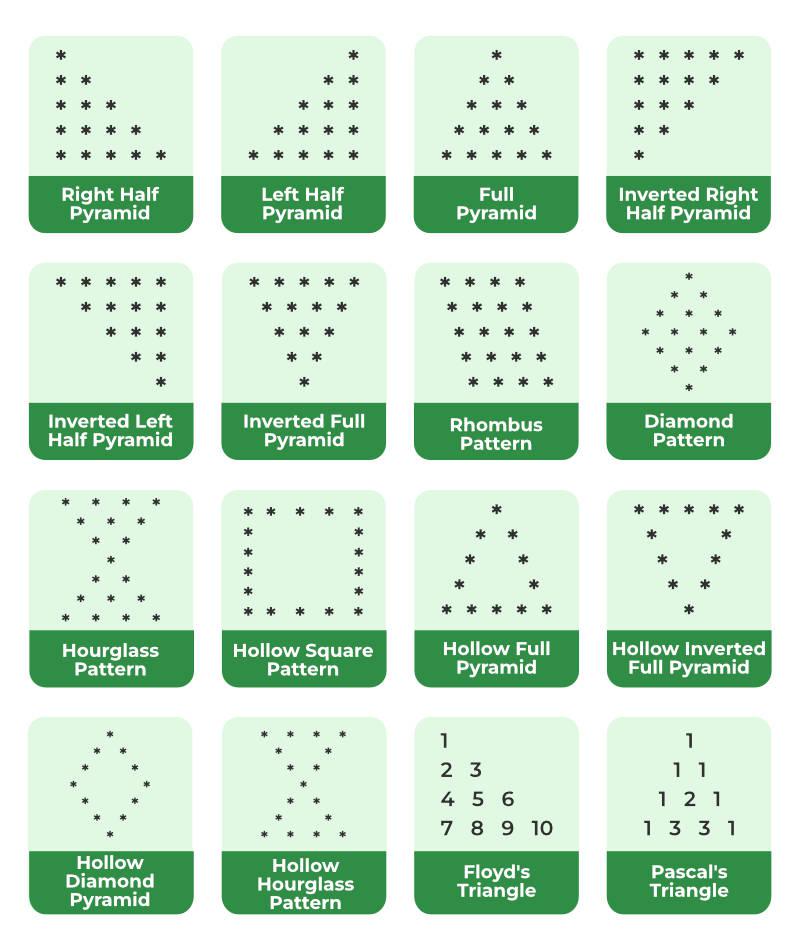
*Geeksforgeeks.org
Square Pattern: Pattern 1
One of the most fundamental number patterns is the square pattern. Printing a square with numbers ranging from 1 to N is required, where N is the total number of rows and columns.
Example
#include <stdio.h>
int main() {
int N, i, j;
printf(“Enter the number of rows and columns: “);
scanf(“%d”, & N);
for (i = 1; i <= N; i++) {
for (j = 1; j <= N; j++) {
printf(“%d “, j);
}
printf(“\n”);
}
return 0;
}
Output
Enter the number of rows and columns: 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
Explanation
In the square pattern of the C programming number pattern, the programmer is asked the number of rows and columns. The inner loop handles the number of columns, and the outer loop manages the number of rows. Each time the inner loop iterates, the column number represented by the variable ‘j’ is shown.
Hollow Square Pattern: Pattern 2
The hollow square pattern consists of printing a square of numbers with an asterisk (*) border and a number-filled inside.
Explanation
#include <stdio.h>
int main() {
int N, i, j;
printf(“Enter the number of rows and columns: “);
scanf(“%d”, & N);
for (i = 1; i <= N; i++) {
for (j = 1; j <= N; j++) {
if (i == 1 || i == N || j == 1 || j == N)
printf(“* “);
else
printf(“%d “, j);
}
printf(“\n”);
}
return 0;
}
Output
Enter the number of rows and columns: 5
* * * * *
* 1 2 3 *
* 1 2 3 *
* 1 2 3 *
* * * * *
Explanation
This program generates a square of integers similar to the square pattern. Instead of writing the number, it displays an asterisk (*) if the current location (first row, final row, first column, or last column) is near the square’s edge.
Pascal’s Triangle Pattern: Pattern 3
Pascal’s Triangle is an array of binomial coefficients formed like a triangle. The two numbers directly above it sum to each number in the triangle.
Example
#include <stdio.h>
int binomialCoeff(int n, int k) {
if (k == 0 || k == n)
return 1;
return binomialCoeff(n – 1, k – 1) + binomialCoeff(n – 1, k);
}
int main() {
int rows, i, j;
printf(“Enter the number of rows: “);
scanf(“%d”, & rows);
for (i = 0; i < rows; i++) {
for (j = 0; j <= i; j++) {
printf(“%d “, binomialCoeff(i, j));
}
printf(“\n”);
}
return 0;
}
Output
Enter the number of rows: 5
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Explanation
We define a function called binomialCoeff, which uses a recursive procedure to calculate the binomial coefficient. The user is invited to enter the number of rows in the main programme. The program uses the binomialCoeff function to generate and output Pascal’s Triangle using two nested loops.
Floyd’s Triangle: Pattern 4
Each row of Floyd’s Triangle has one more natural number than the row before it. It is a right-angled, triangular array of natural integers.
Example
#include <stdio.h>
int main() {
int rows, i, j, num = 1;
printf(“Enter the number of rows: “);
scanf(“%d”, & rows);
for (i = 1; i <= rows; i++) {
for (j = 1; j <= i; j++) {
printf(“%d “, num);
num++;
}
printf(“\n”);
}
return 0;
}
Output
Enter the number of rows: 5
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
Explanation
The number of rows must be specified by the programmer. The program uses two stacked loops to produce and print Floyd’s Triangle. The variable num tracks the current number to be displayed.
Pyramid Pattern: Pattern 5
The pyramid pattern involves printing an incremental pyramidal shape.
Example
#include <stdio.h>
int main() {
int N, i, j;
printf(“Enter the number of rows: “);
scanf(“%d”, & N);
for (i = 1; i <= N; i++) {
for (j = 1; j <= N – i; j++) {
printf(” “);
}
for (j = 1; j <= i; j++) {
printf(“%d “, j);
}
printf(“\n”);
}
return 0;
}
Output
Enter the number of rows: 5
1
1 2
1 2 3
1 2 3 4
1 2 3 4 5
Explanation
The number of rows must be specified by the user. The first inner loop includes printing the gaps required for the numbers to be properly aligned. On each iteration of the outer loop, the second inner loop prints the integers 1 through ‘i’ in ascending order.
Diamond Pattern: Pattern 6
The diamond pattern includes printing a mathematically generated diamond form.
Example
#include <stdio.h>
int main() {
int N, i, j;
printf(“Enter the number of rows: “);
scanf(“%d”, & N);
for (i = 1; i <= N; i++) {
for (j = 1; j <= N – i; j++) {
printf(” “);
}
for (j = 1; j <= i; j++) {
printf(“%d “, j);
}
printf(“\n”);
}
for (i = N – 1; i >= 1; i–) {
for (j = 1; j <= N – i; j++) {
printf(” “);
}
for (j = 1; j <= i; j++) {
printf(“%d “, j);
}
printf(“\n”);
}
return 0;
}
Output
Enter the number of rows: 5
1
1 2
1 2 3
1 2 3 4
1 2 3 4 5
1 2 3 4
1 2 3
1 2
1
Explanation
The code for the pyramid pattern may be modified to generate the diamond pattern. Following the printing of the pyramid form, the lower half of the diamond is printed with a reverse loop.
Spiral Pattern: Pattern 7
The spiral pattern consists of spirally printing a square matrix.
Example
#include <stdio.h>
#define N 4
void printSpiral(int matrix[N][N]) {
int i, k = 0, l = 0;
while (k < N && l < N) {
for (i = l; i< N; i++) {
printf(“%d “, matrix[k][i]);
}
k++;
for (i = k; i< N; i++) {
printf(“%d “, matrix[i][N – 1]);
}
N–;
if (k < N) {
for (i = N – 1; i>= l; i–) {
printf(“%d “, matrix[N – 1][i]);
}
N–;
}
if (l < N) {
for (i = N – 1; i>= k; i–) {
printf(“%d “, matrix[i][l]);
}
l++;
}
}
}
int main() {
int matrix[N][N] = {{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}};
printSpiral(matrix);
return 0;
Output
1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
Explanation
The program has a function named printSpiral, which spirally prints the input matrix. It uses four loops, each representing a side of the square matrix, together with a while loop. The spiral limits are tracked using the loop variables k, l, and N.
Other Number Patterns
Rhombus Pattern
The Rhombus pattern is identical to the square pattern, with the exception that gaps must be added before each line, and their number reduces progressively as the rows increase.
Example
#include <stdio.h>
int main() {
int rows = 5;
// first outer loop to iterate through each row
for (int i = 0; i < rows; i++) {
// first inner loop to print white spaces
for (int j = 0; j < rows – i – 1; j++) {
printf(” “);
}
// second inner loop to print * star in each row
for (int k = 0; k < rows; k++) {
printf(“* “);
}
printf(“\n”);
}
return 0;
}
Output
* * * * * | 1 2 3 4 5 | A B C D E
* * * * * | 1 2 3 4 5 | A B C D E
* * * * * | 1 2 3 4 5 | A B C D E
* * * * * | 1 2 3 4 5 | A B C D E
* * * * * | 1 2 3 4 5 | A B C D E
Hourglass Pattern
The Hourglass pattern is a mixture of the inverted full pyramid and full pyramid patterns, although in the opposite meaning of the diamond design. We’re going to join them in utilising their tips.
#include <stdio.h>
int main() {
int rows = 5;
// first outer loop to iterate each row
for (int i = 0; i < 2 * rows – 1; i++) {
// assigning comparator
int comp;
if (i < rows) {
comp = 2 * i + 1;
} else {
comp = 2 * (2 * rows – i) – 3;
}
// first inner loop to print leading spaces
for (int j = 0; j < comp; j++) {
printf(” “);
}
// second inner loop to print star *
for (int k = 0; k < 2 * rows – comp; k++) {
printf(“* “);
}
printf(“\n”);
}
return 0;
}
Output
* * * * * * * * * | 1 2 3 4 5 6 7 8 9 | A B C D E F G H I
* * * * * * * | 1 2 3 4 5 6 7 | A B C D E F G
* * * * * | 1 2 3 4 5 | A B C D E
* * * | 1 2 3 | A B C
* | 1 | A
* * * | 1 2 3 | A B C
* * * * * | 1 2 3 4 5 | A B C D E
* * * * * * * | 1 2 3 4 5 6 7 | A B C D E F G
* * * * * * * * * | 1 2 3 4 5 6 7 8 9 | A B C D E F G H I
Conclusion
For algorithm thinking and problem-solving abilities, the number pattern in C programming plays an important part. There are numerous patterns to create in C and C++ programming that will help users create the desired output to carry out their algorithms. Learning number patterns in C programming can offer a competitive edge in the world of computer applications.
If you want to enhance your career in the field of computer applications, you can pursue the Master Of Computer Applications (MCA) Online Degree Programme from Manipal University, Jaipur. With this course, you can be well-versed in cloud technology, machine learning, cloud infrastructure, application development and more. To create a balance between your personal/professional lives, this course allows you to attend classes from the comfort of your home so that you can learn at your own pace. To know more about this program, register with Jaro Education.











