Recursion in Data Structures: Types, Algorithms, and Applications
Table of Contents
- Jaro Education
- 20, June 2025
- 11:00 am
If you’re a computer science student, you must be familiar with the term recursion, which is used not only in data structures but also in many programming languages, including C.
In this blog, we will discuss recursion in data structures—its types, algorithms, and some real-world applications.
But let’s understand what recursion is, exactly.
In data structures, recursion is a method where a function repeatedly calls itself. It involves breaking down a complex problem into smaller, more manageable sub-problems, solving each one in turn. For recursion to work effectively, there must be a termination condition to stop the recursive calls. Often viewed as an alternative to iteration, recursion in data structures provides a concise way to tackle complex issues, simplifying the code and making it easier to read compared to iterative solutions.
Understanding Recursion in Data Structures With an Example
Recursion in data structures refers to a method in programming in which a function is able to call itself when solving the problem. This is useful because if there is a complex issue, recursion will help by breaking the complex issue into similar smaller issues until they are manageable. This is similar to peeling an onion; as you peel a layer, the next layer is apparently simpler than the layer preceding it.
In visualising recursion in a data structure, think of being between two mirrors reflecting each other infinitely, each mirroring being a function invocation, and the left reflected is a chain of invocations, but recursion does not continue on forever; it needs a base case in order to terminate the process and prevent an infinite loop.
Example: Calculating Factorial
A classic example of recursion is calculating the factorial of a number. Let’s calculate the factorial of 5 (denoted as 5!). The factorial of a number n is defined as:
n!=n×(n−1)!n! = n \times (n-1)! n!=n×(n−1)!
For 5, this translates to:
5!=5×4×3×2×15! = 5 \times 4 \times 3 \times 2 \times 1 5!=5×4×3×2×1
In recursive terms, we can express this as:
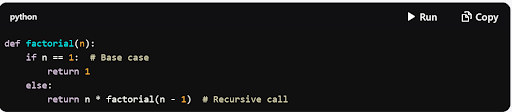
In this function:
- The base case is when nnn equals 1. At this point, the recursion stops, returning 1.
- Each recursive call reduces the problem size, moving towards the base case. For example, factorial(5) calls factorial(4), which calls factorial(3), and so on, until it reaches factorial(1).
How It Works:
- First Call: factorial(5) calls factorial(4)
- Second Call: factorial(4) calls factorial(3)
- Third Call: factorial(3) calls factorial(2)
- Fourth Call: factorial(2) calls factorial(1)
- Base Case Reached: factorial(1) returns 1
Now, the recursion in the data structure unwinds:
- factorial(2) returns 2×1=22 \times 1 = 22×1=2
- factorial(3) returns 3×2=63 \times 2 = 63×2=6
- factorial(4) returns 4×6=244 \times 6 = 244×6=24
- Finally, factorial(5) returns 5×24=1205 \times 24 = 1205×24=120
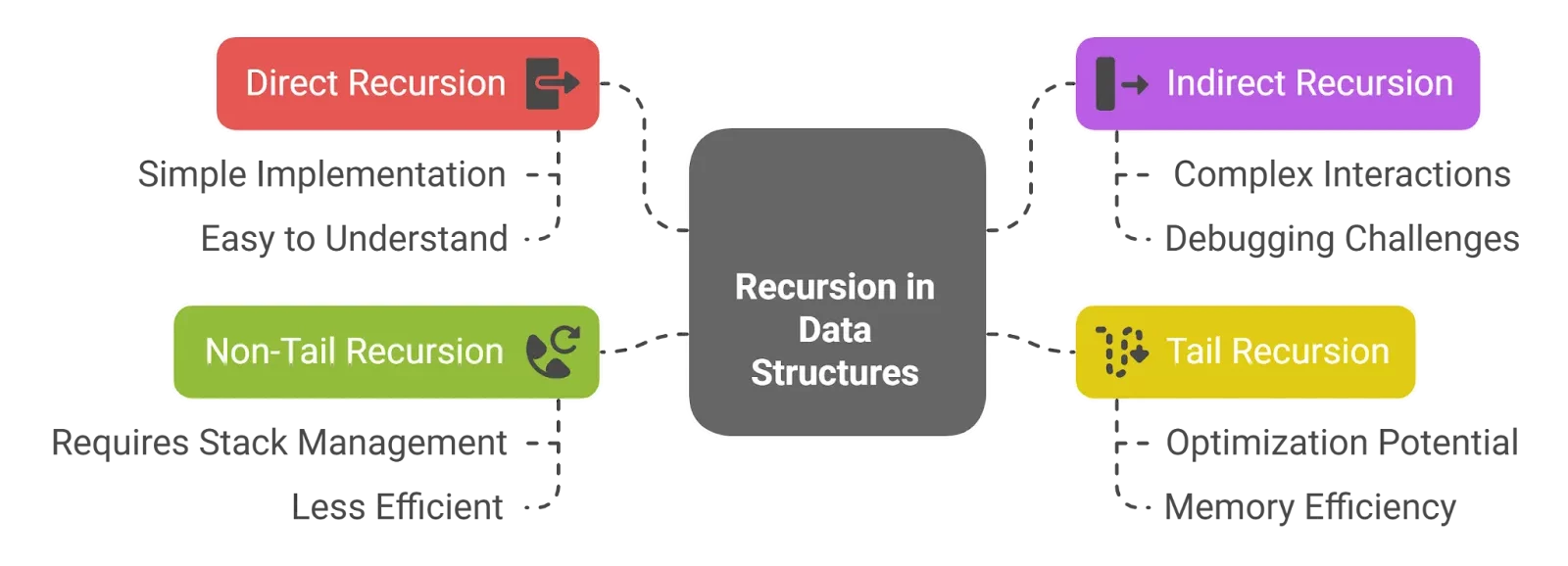
Types of Recursion in Data Structures
*upgrad.com
There are four main types of recursion in data structures. Let’s discuss each one of them in detail:
Direct Recursion
Direct recursion in a data structure occurs when a function calls itself directly within its own definition. This type is straightforward and commonly used. For example, in calculating factorials, as shown earlier, each function call reduces the problem size until it reaches the base case.
To better understand this definition, look at the structure of a direct recursive program.
int fun(int z){
fun(z-1); //Recursive call
}
In this program, you have a method named fun that calls itself again in its function body. Thus, you can say that it is directly recursive.
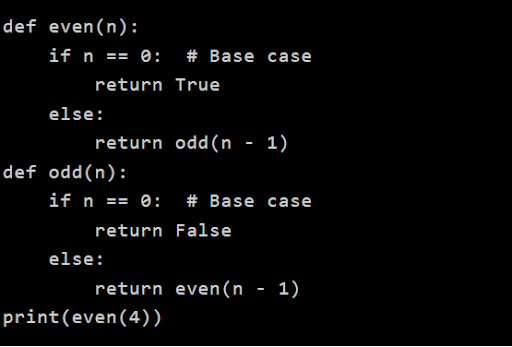
Indirect Recursion
Indirect recursion happens when one function invokes another function, which subsequently calls back the first function. This forms a cycle among multiple functions, resulting in recursive calls.
Here are some common scenarios where indirect recursion in the data structure is utilised:
- Multi-Step Problems: It is often employed in situations requiring collaboration between two or more functions.
- Mutual Recursion: This type of recursion is prevalent in tasks where functions rely on one another to complete their operations.
- Complex Logical Flows: While it introduces added complexity, indirect recursion can provide solutions for sophisticated logical sequences.
- Compiler Design and Expression Evaluation: Indirect recursion is frequently used in these contexts to manage intricate processing tasks.
- Function Call Tracking: It necessitates meticulous monitoring of function calls to ensure clarity and prevent confusion.
Example :
Tail Recursion
If a recursive call (invocation of the same function within the function) is accomplished, that is all that happens! It is followed directly by a return statement, which immediately returns the result of the recursive call with nothing else executed afterwards.
A tail call structure allows optimisations — like Tail Call Optimisation (TCO) — where the compiler, or interpreter, can “re-use” the frame of stack space of the current function. This saves memory and optimises the recursion.
Example of Tail Recursion:
def factorial(n, result=1):
if n == 1: # Base case
return result
return factorial(n – 1, n * result) # Recursive call is the last operation
print(factorial(5))
Output: 120
Non-tail Recursion
Non-tail recursion is when the recursive call is not the final work done in the function. After the call returns, there is potentially more work to do that requires a separate stack frame. Each recursive call will consume memory, resulting in additional memory consumption. Therefore, deep recursion is subject to a stack overflow. Typically, non-tail recursion is also less efficient than tail recursion when the return value is directly returned without further processing.
Example of Non-Tail Recursion:
def factorial(n):
if n == 1: # Base case
return 1
return n * factorial(n – 1) # Recursive call is not the last operation
print(factorial(5))
Output is: 120
Applications of Recursion Algorithms in Data Structures
Recursive algorithms are important in computer science, particularly in examining tree data structures and manipulating them. They offer elegant solutions to the various traversal methods, such as preorder, inorder, and postorder. They also offer solutions to complicated problems on trees and graphs, such as height and shortest path. Understanding the concept of a function calling itself will allow us to better implement complex data structures like linked lists and binary trees. Although recursive algorithms have clear, concise definitions, we must assess their efficiency in terms of time and space complexity, especially in terms of the call stack.
Traversing Trees and Graphs
Recursion is frequently used for traversing and searching data structures like trees and graphs. By leveraging recursive algorithms, we can systematically explore all nodes or vertices, ensuring that we cover every part of the structure.
Tree Traversals
In trees, recursive methods facilitate three primary traversal strategies:
- Preorder Traversal: The algorithm will visit the root node first and recursively call the left subtree, followed by the right subtree. This algorithm is useful for creating a copy of the tree or for generating a prefix expression.
- Inorder Traversal: The method visits the left subtree first, followed by the root node, and finally the right subtree. This method is effective for binary search trees since it yields values in sorted order.
- Postorder Traversal: The algorithm visits the left and right subtrees before visiting the root node. This type of traversal is useful for deleting trees or for creating postfix expressions.
Graph Traversals
Recursion allows for Depth First Search (DFS) in graphs, which extends as far as it can down a path in the graph before backing up. It is an important exploration strategy for pathfinding and checking for cycles in graphs. Additionally, recursion, as opposed to iterative approaches, simplifies the implementation of DFS, since the recursive function already keeps track of already visited nodes.
Sorting Algorithms
Recursion also plays a significant role in sorting algorithms. Notable examples include Quicksort and Mergesort, both of which utilise recursive techniques to sort data efficiently.
- Quicksort: This algorithm selects a pivot element and partitions the array into two subarrays, one with elements less than the pivot and another with elements greater. Each subarray is then sorted recursively, leading to an efficient sorting process with an average time complexity of O(nlogn)O(n \log n)O(nlogn).
- Mergesort: This algorithm divides the data into smaller subarrays, sorts each smaller array recursively, and then merges them back together. Mergesort is known for its stable sorting and consistent performance, operating in O(nlogn)O(n \log n)O(nlogn) time.
Divide-and-Conquer Algorithms
Many divide-and-conquer algorithms utilise recursion to partition problems into smaller, simpler subproblems. One prominent example is the binary search algorithm, which searches for an element in a sorted array by iteratively halving the search interval. The logarithmic algorithm systematically reduces the problem size over time through repeated recursive calls.
Fractal Generation
Recursion is also instrumental in generating fractals—complex shapes that exhibit self-similarity at different scales. For instance, the Mandelbrot set can be created by repeatedly applying a recursive formula to complex numbers. This fascinating application illustrates how recursion can produce intricate visual patterns from simple mathematical rules.
Backtracking Algorithms
Backtracking algorithms often employ recursion to explore possible solutions to problems that require a sequence of decisions. These algorithms systematically search through all potential paths, backtracking when a path fails to lead to a valid solution. Common use cases include solving puzzles like Sudoku or navigating mazes. The recursive nature of backtracking allows for elegant and concise implementations.
Conclusion
In this guide to recursion in data structures, you learnt what recursion is and explored different types of recursion, algorithms, and their applications. If you’re looking for more in-depth learning covering all aspects of data structures, we recommend registering for online certification courses through Jaro Education. We are India’s leading online higher education and upskilling company, bridging the gap between the online education system and students. We offer over 150 management, technology, and techno-functional programs in collaboration with top-reputed institutes.
Frequently Asked Questions
Trending Blogs
