
Our Academic Partners
Find a Program made just for YOU
We'll help you find the right fit for your solution. Let's get you connected with the perfect solution.

Is Your Upskilling Effort worth it?
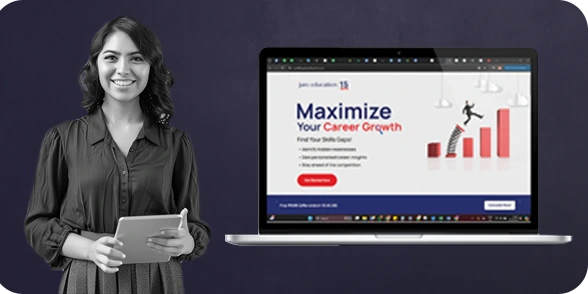
Are Your Skills Meeting Job Demands?
Experience Lifelong Learning and Connect with Like-minded Professionals
Trending Courses
Access a wide range of certification programs from IITs and IIMs, designed to bridge the gap between industry needs and academia.
Jaro Education Awards & Achievements
A testament to our commitment to shaping the futures of working professionals through Online education.




Latest News & Updates








Maximize your Career Growth with AI
Skill Gap Analysis Meets Career ROI — Invest in What Actually Boosts Your Worth
Skill Gap Calculator
Find out what you’re missing to land your dream role. Understand where you stand with a detailed comparison of your skills against industry demands.
ROI Calculator
Find out exactly how much your next career move is worth. Our ROI calculator helps you compare your current earning potential with what you could achieve after upskilling.

















































































