Bias – Variance Tradeoff In Machine Learning: Concepts & Tutorials, Real Time Examples

Prediction errors can be divided into three constituents, namely bias errors, variance errors, and irreducible errors. Bias errors occur when there is high bias in the data, which can result in underfitting and incorrect predictions. Bias errors can be considered to be associated with models, which is basically the cornerstone for bias-variance trade-off. 

Variance error degree measures to what extent the predicted values of the model change when varying the training set. Flexible models may capture noise rather than actual patterns, which leads to overfitting. Controlling variance is important in the bias-variance trade-off. Reducing variance implies reducing the model complexity.

Irreducible errors are basically noise in the data that could be errors of measurement or variables that are inherently unpredictable. These errors cannot be reduced by any model, establishing a floor on the performance level that can be reached. In performing the calculation for the total error, you need to consider the irreducible errors in optimizing the bias variance trade-off.

Model complexity is at the center of the balance that exists. As model complexity increases, the bias decreases and the variance increases. This is what underlies the whole idea of the bias-variance trade-off.

High bias often arises due to underfitting: The model is too simple to model the true relationship between the input features and the output variables. This can occur in cases where significant features are left out, the time taken for training is not sufficient, or when there is a lack of flexibility in the algorithm applied. The bias variance trade off in machine learning discusses this problem very commonly. 

Models suffering from high bias typically have high generalization error across both the training and testing data. They cannot improve further with the use of additional data, essentially highlighting how the structure of the model is limiting learning itself. All such traits make high-bias models quite predictable but inaccurate, which is an important point of Bias Variance Trade-off in Machine Learning.

Some algorithms are more susceptible to bias owing to their simplicity. Bias variance tradeoff examples include linear regression on non-linear data, Naïve Bayes with strong independence assumptions, and shallow decision trees with limited depth. These models often struggle with complex datasets, reinforcing the importance of understanding the bias variance trade off in machine learning.

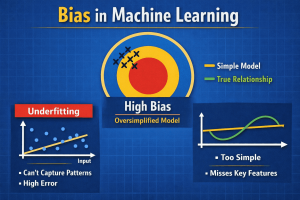
A real-world bias variance tradeoff example of a biased model is in housing price prediction using just square footage and ignoring the location or amenities. Visually, this may be thought of as a straight line trying to fit curved or scattered data points-an intuitive way of illustrating bias, and its role in the bias variance trade off in machine learning.

High variance often comes from overfitting. This happens when a model is overly complex compared to the amount of training data available. Deep decision trees, high-degree polynomial models, or neural networks with many parameters can memorize training data instead of learning general patterns. This increases variance and intensifies the bias-variance trade-off in machine learning.

Models with high variance usually perform very well on training data but poorly on validation or test datasets. Small changes in input data can cause significant fluctuations in predictions, making these models unstable. This behavior clearly indicates an imbalance in the bias-variance trade-off in machine learning.

Some algorithms are more likely to have high variance, such as unpruned decision trees, k-nearest neighbors with very small values of k, and complex neural networks without regularization. These models need careful tuning to manage variance and effectively address the bias-variance trade-off in machine learning.  

A real-world example of variance issues appears in stock price prediction models trained on limited historical data, where predictions change significantly with new inputs. Increasing the size and diversity of training data typically reduces variance, as more examples help stabilize learning within the bias-variance trade-off in machine learning.

Key Differences:

Definition:

• Bias: Error from overly simple assumptions, leading to underfitting.
• Variance: Error from sensitivity to training data, leading to overfitting.

Model Complexity:

• Bias: Common in simple models that fail to capture complex patterns.
• Variance: Common in complex models that fit training data too closely. 

Performance:

• Bias: Poor performance on both training and test data.
• Variance: Great performance on training data but poor performance on unseen test data.

Learning Behavior:

• Bias: Model underfits, missing significant relationships in the data.
• Variance: Model overfits, treating noise like it’s important information. 

Practical Implications for ML Engineers:

Engineers must balance bias and variance to improve model generalization. High bias may need more features or more complex algorithms, while high variance might need regularization or more training data. This highlights the essential nature of the bias-variance trade-off in machine learning. 

This understanding helps with effective model selection, tuning, and deployment in real-world ML systems.

A way to think about total error is as a mixture: bias squared plus variance plus irreducible error. This can be written down as equations, but the punchline is easy to state: to reduce bias, variance goes up, and vice versa. It is this seesaw by which the bias/variance trade-off is captured. 

As the models grow in complexity, they will fit more patterns in the data, and therefore, the bias will reduce. For a model to reduce bias, it either needs to be complex, increasing the variance, or it needs to be regularized. The relationship between bias and variance typically occurs in a U-shape, implying that if a model is either biased or variable, its overall error will be high. 

In most cases, perfectly balancing bias error and variance is impossible. This is due to data that is noisy and cannot be easily predicted. This is compounded by real-world constraints, such as CPU capabilities when it comes to computing costs.

– Complexity is low. The model is not complex enough to understand what is actually happening. The model is not recognizing patterns, and it’s biased and varies less. It’s not adapting to the data, and its errors will remain large.

– Sweet spot: In the middle is the optimal level of complexity where bias and variance are just balanced and the total amount of error is lowest. This is what most practitioners pursue.  

– High complexity: This is where the model tends to overfit the training set or, in other words, fits the training set too closely. This makes the bias decrease and the variance increase, leading to poor performance on unseen data points. 

In practical applications, data is never clean or nicely behaved. Noises, missing values, and wild variations make the bias-variance tradeoff more of a rule of thumb than a simple recipe. It is better to use your knowledge and visual insight into whether you need to reduce the complexity of your model, get more data, and/or use regularization.

Example 1: Linear Regression vs Polynomial Regression

In predicting housing prices, a linear regression model assumes a straight-line relationship between features like square footage and price. This simplicity often leads to high bias because the model cannot capture complex, non-linear patterns in the data. Using polynomial regression allows for more flexibility. A low-degree polynomial might underfit, while a high-degree polynomial fits the training data perfectly, which leads to high variance and poor generalization. The bias-variance tradeoff is illustrated by choosing an optimal polynomial degree that balances flexibility and stability, minimizing total prediction error. 

Example 2: Decision Trees

Decision trees are easy to interpret, but their depth greatly affects bias and variance. Shallow trees make broad, simplistic splits, which leads to biased predictions that underfit the data. In contrast, deep trees memorize the training data, capturing noise and resulting in high variance. One practical solution is pruning, which simplifies the tree by removing unnecessary branches. This method shows the bias-variance tradeoff by managing overfitting while keeping predictive power.  

Example 3: K-Nearest Neighbours (KNN)

KNN predictions rely on the number of neighbors considered. High K values smooth out predictions by averaging over many points, leading to high bias and underfitting. Low K values make the model overly sensitive to individual training points, causing high variance and overfitting. Choosing an intermediate K offers a practical balance, clearly illustrating the bias-variance tradeoff in a straightforward way.

In all these scenarios, the bias-variance tradeoff highlights an important principle: no model can achieve zero bias and zero variance at the same time. Practitioners must carefully adjust model complexity, apply regularization, or use techniques like pruning and cross-validation to reach optimal generalization. Real-world machine learning involves navigating this tradeoff to provide reliable, robust predictions across different datasets.

Two common forms of regularisation are L1 (Lasso) and L2 (Ridge). L1 regularisation adds the absolute values of model coefficients to the loss function. It encourages sparsity by pushing some weights to zero, making the model simpler. L2 regularisation adds the squared values of coefficients. This reduces the impact of individual features without removing them. Both methods help manage the bias-variance tradeoff, but in different ways. L1 is useful for selecting features, while L2 stabilizes predictions.  

Regularisation affects bias and variance in different ways. Increasing regularisation strength lowers variance by preventing overfitting but raises bias, which can lead to underfitting. Choosing the right regularisation strength often involves cross-validation to find the best balance.  

Practical applications include predicting housing prices with linear regression or forecasting customer churn using logistic regression. L2 regularisation can reduce overfitting to noisy features, while L1 can identify the most relevant predictors. In summary, regularisation is an important tool for managing the bias-variance tradeoff in machine learning. It helps ensure that models generalize well to new data.

Large datasets help reduce variance by giving the model more examples to learn from. This lets the model focus on general patterns instead of noise. Strategies like early stopping, which means stopping training before overfitting happens, and dropout, which randomly disables neurons during training, are effective in managing variance while keeping bias low. 

Even with overparameterization, deep learning models often generalize quite well. This behavior is partly due to modern optimization methods and regularization techniques. Understanding these details is important for controlling the bias-variance tradeoff in machine learning, especially in complex models with high capacity.

Cross-validation is essential to give an idea of the behavior of the model when dealing with unseen examples, if it is the right time to adjust the model’s complexity or the level of regularized terms. Monitoring the learning curve can give an idea if the model suffers from underfitting or overfitting. 

Ensemble learning concepts such as bagging and boosting allow leveraging strengths of other models to minimize bias and variance and help in generalization of results. It is important to continue testing in the production environment as well because by using new data available, you can re-weight the bias and variance.

These methodologies assist machine learning engineers in developing models with good generalization capabilities and the ability to maintain consistency and resist noise.

The bias-variance tradeoff in machine learning is a key concept for building reliable and generalizable models. Bias refers to errors from overly simple models, while variance indicates errors from overly complex, sensitive models. Understanding how they interact helps practitioners make smart choices about model selection, complexity, and regularization. 

Knowing this tradeoff improves model reliability by guiding feature selection, hyperparameter tuning, and evaluation methods. Using techniques like cross-validation, regularization, ensemble learning, and monitoring learning curves ensures that models perform well on both training and unseen data. 

For machine learning practitioners, the main takeaway is that achieving a perfect bias-variance balance is seldom possible, but careful management can lead to better generalization. Mastering this tradeoff is not just a theoretical exercise—it significantly affects the strength, scalability, and success of ML models in real-world situations.